Cálculos combinados

Para resolver los cálculos combinados necesitamos saber el orden de las operaciones :

• Orden de las operaciones
• Cuando en un calculo en el que no hay paréntesis figuran distintas operaciones, se resuelven en este orden:
• 1º- Raíces y potencias.
• 2º- Multiplicaciones y divisiones.
• 3º- sumas y restas.

• Por eso, es muy importante separar en términos antes de resolver un calculo combinado. Los signos que separan términos son + y - 

• Si hay paréntesis, hay que resolver primero las operaciones que están dentro de ellos, respetando el orden mencionado antes. Si en un radicando hay cálculos combinados, también se resuelven en el orden establecido.

Criterios de divisibilidad

• Los criterios de divisibilidad son reglas que nos sirven para saber si un número es divisible por otro sin necesidad de realizar la división .

M.C.M y M.C.D

M.C.M= MÚLTIPLO COMÚN MENOR 

M.C.D= MÁXIMO COMÚN DIVISOR

Para hallar el M.C.M o el M.C.D lo primero que tenemos que hacer es factorizar los números que utilizaremos.Hay dos formas de hacerlo, pero para ambas necesitaremos saber que son los números primos y compuestos.

• Un número es primo si tiene solo cuatro divisores enteros: el mismo, su opuesto, uno y menos uno .
• Un numero es compuesto cuando tiene más de cuatro divisores.

• Primer forma de factorizar:

• Segunda forma:

• Para hallar el M.C.M debemos multiplicar los factores comunes y no comunes que nos quedan de la factorizacion con su mayor exponente.
• Para hallar el M.C.D multiplicamos solo los factores comunes que nos quedan de la factorizacion con su menor exponente. 

 para no estar dudando cuando estas en la evaluación ...


... o para no tener que ir a la escuela en diciembre 
...
 
...o para no estar todo el día estudiando que no es muy agradable pero hay que hacerlo igual...


... y para lo mas importante poder disfrutar de las vacaciones...
 


... hace como nosotros y lee estos contenidos que te van a ayudar mucho.

ecuaciones

Una ecuación es toda igualdad que contiene uno o más números llamados incógnitas.
resolver una ecuación es encontrar el valor de la incógnita que hace verdadera la igualdad por ejemplo:
 X . (-2) + 18 : 2 - 5 = 8
X . (-2) + 9 -5 = 8
X . (-2) + 4 = 8
X . (-2) + 4  + 4 - 4 = 8 - 4
X . (-2) : (-2) = 4 : (-2)
X= -2

VERIFICACIÓN

(-2) . (-2) + 18 : 2 - 5 = 8
    4 + 9 - 5 = 8
         13 - 5 = 8 

Graficos

                                                                                                                                                                               Funciones:
En matematicas se dice que una magnitud o cantidad es funcion de otra si el valor de la primera depende del valor de la segunda.

•  Las funciones se representan en gráficos cartesianos. El eje horizontal se llama eje de abscisas y el eje vertical eje de ordenadas.
• X es la variable independiente y Y es la variable dependiente 

                              





Hay situaciones en las cuales se relacionan dos variables y puede establecerse que una de ellas depende de la otra. Es así como una variante se conoce con el nombre de variable independiente en tanto que la otra se la designa con el nombre de variables dependiente.

• Por ejemplo el tiempo podría ser una variable independiente y el crecimiento de un bebe depende del tiempo, o la distancia de un camión con respecto a un punto de referencia podría depender de tiempo de marcha, es lo mismo que decir que la distancia esta en función del tiempo.
• A cada valor de la variable independiente le corresponde un único valor de la variable dependiente a este tiempo de correspondencia que relacionan  dos variables se la llama funciones. 

 Cuando en un eje de un gráfico aparecen dibujadas dos rallitas significa que el eje se corto.

En una funciona dom F se llama dominio al conjunto de valores de variable independiente que tienen imagen a través  de esa función. Se lo simboliza con (F).
Se denomina conjunto imagen al conjunto de valores de la variable dependiente que son imagen de algún elemento del dominio a través de esa función. Se simboliza Im(F)

Algunas veces pueden ser representadas por una tabla. En ella únicamente se conocen algunos pares ordenados, es decir, en algunos instantes del proceso que se trata. Este de tablas se denomina tabla de valores.

introducción de variable

un concepto muy importante en matemáticas y en otras ciencias es el de variable, y, en particular, la relación entre variables. tomamos como una primera aproximación a la idea de variable asociada a un valor que puede sufrir ciertas modificaciones.
cuando dos variables se relacionan entre si, el valor de una de ellas depende del de la otra.

Números enteros

El hombre primitivo creó los números cuando necesitó contar y para ello le alcanzaba con los números naturales, pero luego aparecieron muchísimas situaciones, tales como las temperaturas bajo cero, las profundidades en el mar, los saldos deudores en las cuentas bancarias, etc; que hicieron necesaria la creación de otros números: los ENTEROS NEGATIVOS.

El conjunto de los números enteros

Cuando hablamos de nuestro equipo favorito o de un grupo de rock, aparece la idea de conjunto. 

En Matemática también hablamos de conjuntos,y los designamos con letras mayúsculas. Los elementos que pertenecen a un conjunto se anotan entre llaves. Un conjunto esta incluido en otro si todos sus elementos pertenecen también al otro conjunto.  

• Modulo o valor absoluto 

En matemática, a la distancia desde un numero hasta 0 la llamamos modulo o valor absoluto de ese numero.

Como el modulo de un numero es una distancia, nunca puede ser negativo.Si a ese numero lo llamamos 6, lo escribimos así:|6| 

• Suma de números enteros

Para sumar números enteros, vamos a tomar el ejemplo del ascensor. Escribiremos un signo ( +) cada vez que el ascensor sube y un signo (-) cada vez que baja.

Ejemplos

• El ascensor subió 4 pisos, paro y subió otros 3 pisos.En total,subió 7 pisos.

                       Lo indicamos así: (+4) + (+3) = +7

• El ascensor bajo 2 pisos, paro y bajo otros 6 pisos. En total,bajo 8 pisos.

                      Lo indicamos así: (-2) + (-6) = -8 

Cuando sumamos números enteros de igual signo, sumamos los valores absolutos y copiamos ese signo.

• El ascensor estaba en la planta baja, subió 5 pisos, paro y bajo 7 pisos. Finalmente,quedo en el segundo subsuelo.

                     Lo indicamos así : (+5) + (-7) = -2

•  El ascensor estaba en la planta baja,bajo 1 piso,paro y subió 3 pisos. Finalmente, quedo en el segundo piso. 

                   Lo indicamos así: (-1) + (+3)= +2

Cuando sumamos dos números enteros de distintos signos,restamos sus valores absolutos y, al resultado, le asignamos el signo de numero mayor valor absoluto.

• Resta de números enteros

Una resta de números enteros se puede resolver como si se tratara de una suma, pero con una particularidad:

El símbolo de la resta le cambia el signo a la cifra que le sigue, por lo que:

Si el numero que se resta es positivo lo convierte en negativo.

Si el numero que se resta es negativo lo convierte en positivo.

A) A un numero positivo le restamos otro numero positivo:

                                                      3-2 

Lo tratamos como si fuera una suma,pero a la cifra que se le resta (2) le tenemos que cambiar el signo.
                                                    3+(-2)
por un lado sumamos los números positivos (3)
por otro lado los negativos
Ahora el resultado positivo suma y el negativo resta:
                                          3 - 2 =1
B) A un número positivo le restamos un número negativo:
                                         3-(-4)
Lo tratamos como si fuera suma, pero a la cifra que se resta (-4) le tenemos que cambiar el signo
                                         3+(4)
Se trataría de una suma normal:
                                         3+(4)=7
C) A un número negativo le restamos otro numero negativo 
                                        (-3)-(-4)
   Lo tratamos como si fuera una suma, pero a la cifra se le resta (-4) le tenemos que cambiar el signo.
                                        (-3)+(4)
Por un lado sumamos los números positivos: 4
Por otro lado sumamos los números negativos:(-3)
ahora el resultado positivo suma y el negativo resta
                                        4 - 3=1
D) A un número negativo le restamos un numero positivo
                                       (-3) - 4
Lo tratamos como si fuera una suma, pero a la cifra que resta (4) le tenemos que cambiar el signo (-4)
                                      (-3) + (-4)
Se trataría de una suma de dos números negativos. Es una suma normal pero el resultado tiene signo negativo:
                                       (-3) + (-4)  = -7


                                     Propiedades al operar

• Utilizamos las mismas que al hacerlo con números naturales: 
• Propiedad asociativa: podemos agrupar los números de diversas formas y que de el mismo resultado. Esta propiedad se cumple en la suma.
•  En suma: 

-2+5(-8)=

[-2+5]+(-8) = -2+[5+(-8)]

  3 + (-8) = -2+[5-8]

         3-8 =  -2+(-3)

       -5 =  -2-3

   -5 = -5

• En multiplicación:

(-2) . 5 . (-4)=

[(-2) . 5] . (-4) = (-2) . [5 . (-4)]

-10 . (-4) = (-2) . (-20)

40 = 40

• Propiedad conmutativa: se invierte el orden de los números y el resultado no se altera.Esta propiedad no se cumple en la suma.
• en suma:

2+(-3) = (-3)+2

         2-3 = (-3)+2

     -1 = -1

• En multiplicación:

(-3) . 5 = 5 . (-3)

-15 = -15

• Propiedad distributiva: permite descompones los números, distribuirlos, sumarlos o restarlos y el resultado no cambiara. 
• Con resta: 

(-3) . (5+1) = (-3) . 5+ (-3) . 1

(-3) . 6 = -15 + (-3)

-18 = -15-3

-18 = -18 

• Con división:

(6-3) : (-3) = 6 : (-3) + (-3) : (-3)

3 : (-3) = -2 + 1

-1 = -1

• Los números opuestos

Los números que tienen el mismo modulo y distinto signo se llaman opuestos. Por ejemplo:

• Cálculos con enteros: acerca del orden 
• Para resolver los cálculos con las 4 operaciones, primero multiplicamos y dividimos y luego sumamos o restamos.

1+3 . 5-10 = (-2)

1+15-10=(-2)

16-10= 6

• Si en un calculo combinado hay paréntesis, corchetes  y llaves, primero suprimimos los paréntesis luego los corchetes y por ultimo las llaves, luego de realizar las operaciones que estos encierran.
• Los signos 

Ley de los signos que se aplica en los números enteros.

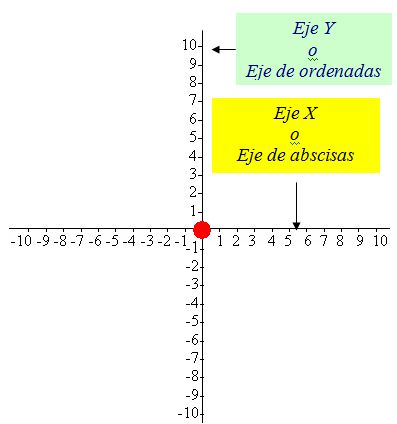
• La recta numérica
• En la recta numérica los valores negativos se ubican a la izquierda del 0. El número -1 esta a una unidad a la izquierda del 0, el -2 a una unidad a la izquierda del -1 y así sucesivamente. 

Al igual que en los números naturales es mayor aquel que se encuentra a la derecha. El 0 es el único número entero que no es positivo ni negativo.

Potencias y Raices

La potenciación  

es una forma abreviada de escribir un producto formado por los mismos factores                                                                                                                                                      

• Si el exponente es 2 se dice "al cuadrado" 
• Si el exponente es 3 se dice "al cubo"

Propiedades de las potencias :

Productos de potencia de igual base: se deja la misma base y se suman los exponentes.

• Cociente de potencias de igual base: se deja la misma base y se restan los exponentes

• Potencia de otra potencia: se multiplican los exponentes

• Propiedad distributiva de la potencia con respecto a la divición: 

• Propiedad distributiva con respecto a la multiplicación: 

Para tener en cuenta :

• Si tenemos 2º (2 elevado a 0) el resultado siempre será 1

                  2º=1             546º=1          53764932º=1

                            

• Si tenemos 54 elevado a la 1 el resultado sera 54 (al igual que con todos los números).

Raíces  

• La radiación , es una operación que "deshace"la potenciación, osea, permite averiguar cual es la base de la potencia. 
• No se puede hallar la raíz cuarta, sexta, octava, etc de un número entero negativo, por que ninguna base negativa elevado a un exponente par da un entero negativo

Propiedades de las raíces

• Propiedad distributiva:

Suma y resta:

Multiplicación y divición

Numeros naturales

un numero natural es cualquiera de los números que se usan para contar los elementos de un conjunto

• Los números naturales se pueden sumar y multiplicar en cualquier orden (propiedad conmutativa) y también se pueden agrupar de cualquier manera (propiedad asociativa)

Por ejemplo:   398 + 17 + 2 = (398+2) + 17 = 400 + 17= 417
                       5 . 93 . 2 = 93 . (5 . 2) = 93.10 = 930

• Se puede aplicar la propiedad distributiva de la multiplicación con respecto a la suma y la resta acelerar cálculos mentales.

  

• La propiedad distributiva en la división con respecto a la suma y la resta se cumple solo "a derecha":
• Por ejemplo: (15-10) : 5  = 15 : 5 - 10 : 5

                                   5 : 5=1  = 3-2=1

• En cambio:  12 : (2+4)  no es igual a 12 : 2 + 12 : 4

                           12 : 6= 2    no es igual a 6+3= 9

• Cualquier número multiplicado por 1 es igual al mismo número.
• Cualquier número multiplicado por 0 da 0.
• No se puede dividir por 0.
• 0 dividido por cualquier número da 0.